Sprachen kennen wir alle aus dem Alltag. Um eine Sprache zu beschreiben, die eine Maschine verstehen
kann, schauen man sich zunächst unsere natürliche Sprache genauer an.
Es gibt Bildungsregeln auf Wort- und Satzebene, in welcher Reihenfolge bestimmte Satzglieder stehen
müssen. Unsere natürliche Sprache ist nicht vollständig eindeutig. Es gibt oft verschiedene
Möglichkeiten einen Satz zu erstellen und trotzdem wird dieser von anderen verstanden. Es können
sogar Teile von Wörtern und Sätzen weggelassen werden und der Inhalt kann in vielen Fällen
verstanden werden. Wenn jemand z. B. in einem lauten Club steht und sich mit einer zweiten Person
unterhält, könnte aufgrund der Lautstärke der Satz: "Na, wie bist du hergekommen?" nur als
"Na, wie...hergekommen?" ankommen. Die zweite Person wird höchstwahrscheinlich verstehen,
was gefragt wurde und kann entsprechend reagieren. Ähnliches kann man bei geschriebener natürlicher
Sprache feststellen. Lässt man z. B. in jedem Wort genau einen Buchstaben weg, wird der
Text sehr wahrscheinlich trotzdem zu lesen sein.
Einer Maschine ist es nur bedingt möglich eine solch mächtige Fehlerkorrektur vorzunehmen,
wenn ihr entsprechende Fähigkeiten programmiert wurden.
Natürliche Sprachen weisen eine umfangreiche Menge an Regeln auf, mit denen auf Wort- und
Satzebene diese Sprache beschrieben wird, die Grammatik, und ebenso umfangreich wird geregelt,
wie aus dem Wörtern Sätze gebildet werden, mit der Syntax. In einer natürlichen Sprache z.
B. geben die Syntaxregeln der Grammatik vor, in welcher Reihenfolge die Satzglieder in einem Satz
angeordnet werden können.
Eine Computersprache ist analog aufgebaut, nur muss alles in solch einer Sprache eindeutig und
korrekt geschrieben sein und darf keinen Interpretationsspielraum lassen. Es gibt verschiedene
Sprachtypen mit steigendem Komplexitätsgrad der Grammatik. Der Sprachwissenschaftler Noam
Chomsky hat 1956 eine Hierarchie von Sprachen aufgestellt, in welcher die formalen Sprachen, für
Maschinen, nicht von den natürlichen Sprachen getrennt betrachtet werden, sondern hinsichtlich
ihrer Wortbildungsregeln mit aufsteigender Komplexität geordnet werden.
Rekursiv aufzählbar
Kontextsensitiv
Kontextfrei
Regulär
Wir betrachten hier nur die Typ 3, regulär und die Typ, kontextfreie, Sprachen.
Die Grammatik einer Sprache kann allgemein, also unabhängig vom Typ in der Hierarchie von Chomsky, als 4-Tupel G={N, T, S, P} modelliert werden, wobei die einzelnen Komponenten nach einigen konkreten Beispiel definiert werden.
| syntaktisch korrekt | syntaktisch inkorrekt | |
|---|---|---|
| Schulnote Sek I | 2+, 4-, 6 | +1, -+4, 32, 6-, 1+ |
| Uhrzeit | 10:05, 23:54, 02:31 | 10::05, 23:5544, 06:89 |
| Autokennzeichen | OS-AB 1234, HH-CD 23, M-E 1 | OS AB 1234, HHCD 23, M 1-E |
| Geklammerter Term | (1+2)*(5-4), 3*(15-4), 9-(2+4) | )1+2)*(5-4), 3()*(15-), 9+-2+4) |
Schulnoten können im Sekundarbereich 1 mit einer Ziffer von 1 bis 6 und mit einem Notenzusatz + oder - angegeben werden. Beginnen muss ein Wort der Sprache "Schulnoten" also mit einer Ziffer
von 1 bis 6 und anschließend kann ein Notenzusatz kommen. Nur 1+ und 6- sind nicht möglich.
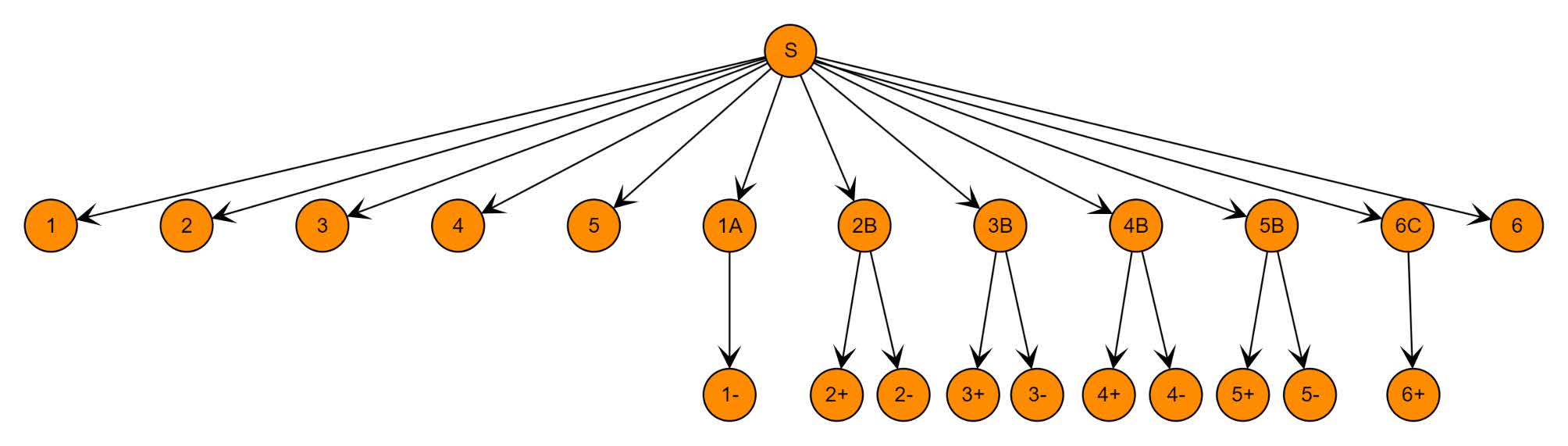
Diese Bildungsregeln kann man grafisch mit einem Syntaxdiagramm oder einem Ableitungsbaum
visualisieren.
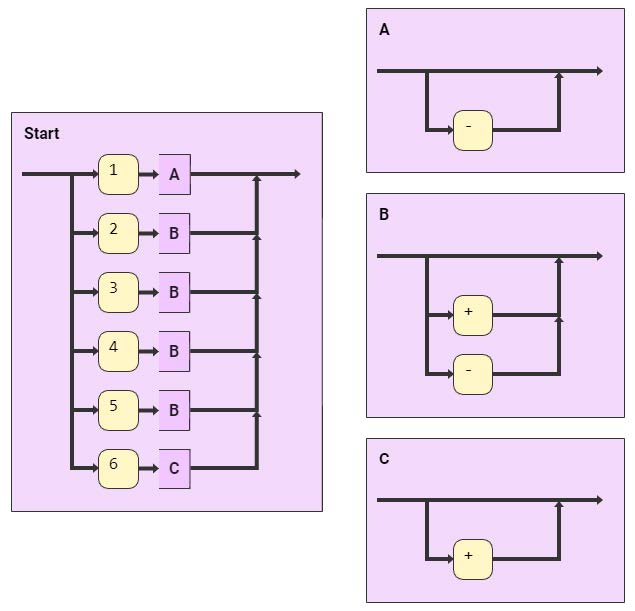
Zur Bildung eines Wortes startet man immer mit einem Startsymbol S, eine Art Variable, die man hier als Nichtterminal bezeichnet. Für unsere Schulnoten kann das S durch ein finales Zeichen, ein Terminal, ersetzt werden (1,...6) oder mit 1,...6 und einer weiteren Variablen A, B oder C, ein weiteres Nichtterminal, rechts davon ersetzt werden. Das Nichtterminal A muss durch -, B muss durch + oder - und C durch + ersetzt werden.
Nun können wir die formale Definition der formalen Sprache Schulnoten als 4-Tupel G={N, T, S, P} angeben.
| Komponente | Definition |
|---|---|
| N | Menge der Nichtterminale für die Erzeugung von Wörtern. Hier N={S, A, B, C} |
| T | Menge der Terminale. Diese sind die Buchstaben oder Silben, die in Wörtern der Sprache vorkommen. Hier T={1, 2, 3, 4, 5, 6, +, -} |
| S | Startsymbol. Eines der Nichtterminale muss als Startsymbol definiert werden. Damit starte die Bildung aller Wörter der Sprache. Hier S |
| P | Produktionsregeln. Diese sind alle Erzeugungsregeln dfer Wörter. Hier: S ➔ 1|2|3|4|5|6|1A|2B|3B|4B|5B|6C A ➔ - B ➔ +|- C ➔ + |
Unser Beispiel zu den Schulnoten ist eine reguläre Sprache. Die Grammatik einer regulären Sprache muss genau einer der beiden folgenden Bedingungen genügen.
|
Eine Grammatik G={N, T, S, P} heißt (rechts-)regulär, wenn alle Produktionsregeln P die
folgende Form haben: Ein Nichtterminal ➔ ein Terminal Bsp.: A ➔ + oder Ein Nichtterminal ➔ ein Terminal und ein Nichtterminal Bsp.: S ➔ 3A |
|
Eine Grammatik G={N, T, S, P} heißt (links-)regulär, wenn alle Produktionsregeln P die folgende
Form haben: Ein Nichtterminal ➔ ein Terminal Bsp.: A ➔ + oder Ein Nichtterminal ➔ ein Nichtterminal und ein Terminal Bsp.: S ➔ A3 |
-
Es soll eine reguläre Grammatik erzeugt werden, die alle Wörter erzeugt, die mit a beginnen und mit a enden. Das Alphabet soll nur aus a und b bestehen.
- Geben Sie zunächst drei korrekte und drei inkorrekte Wörter der Sprache an.
- Entwerfen Sie eine reguläre Grammatik für diese Sprache.
- Beurteilen Sie, ob sich an dem Aufbau der Grammatik etwas ändert, wenn das Alphabet aus allen Buchstaben besteht.
- Geben Sie für das Uhrzeit Beispiel aus dem Einstieg die reguläre Grammatik an, um die Sprache der Uhrzeiten zu erzeugen.
Hier wird später eine Lösung erscheinen.
Hier wird später die Lösung auftauchen.
- Bearbeiten Sie die Aufgaben 1 bis 2.
- Finden Sie mindestens einen Anwendungsfall von regulären Grammatiken aus Ihrem Alltag.
Schauen wir uns noch einmal die Sprache LSchulnoten={N, T, S, P} an, mit N={S, A, B, C}, T={1, 2, 3, 4, 5, 6, +, -}, Startsymbol = S und P:
S ➔ 1|2|3|4|5|6|1A|2B|3B|4B|5B|6C
A ➔ -
B ➔ +|-
C ➔ +
Das Erstellen eines Wortes nach dieser Grammatik ist sehr ähnlich zum Abarbeiten einer Eingabe eines DEA. Das Startsymbol können wir als Startzustand interpretieren. Die Terminale als Eingabealphabet und die Nichtterminale als weitere Zustände. Anhand der Produktionsregeln kann man die Zustandsübergänge konstruieren. Beginnt man mit einer 1, 2, 3, 4, 5 oder 6, wäre das bereits eine korrekte Eingabe, was an den Produktionsregeln für S erkennbar ist. Allerdings können allen diesen Eingabezeichen auch ein weiteres und vor allem nicht immer gleiches zweites Zeichen folgen. Deshalb kann in den Produktionsregeln nach den Notenzahlen auch noch ein Nichtterminal folgen. Davon für 1 ein anderes, als für 2- 5 und noch ein drittes für 6. Deshalb muss es für jedes dieser Nichtterminale einen weiteren Zustand geben:
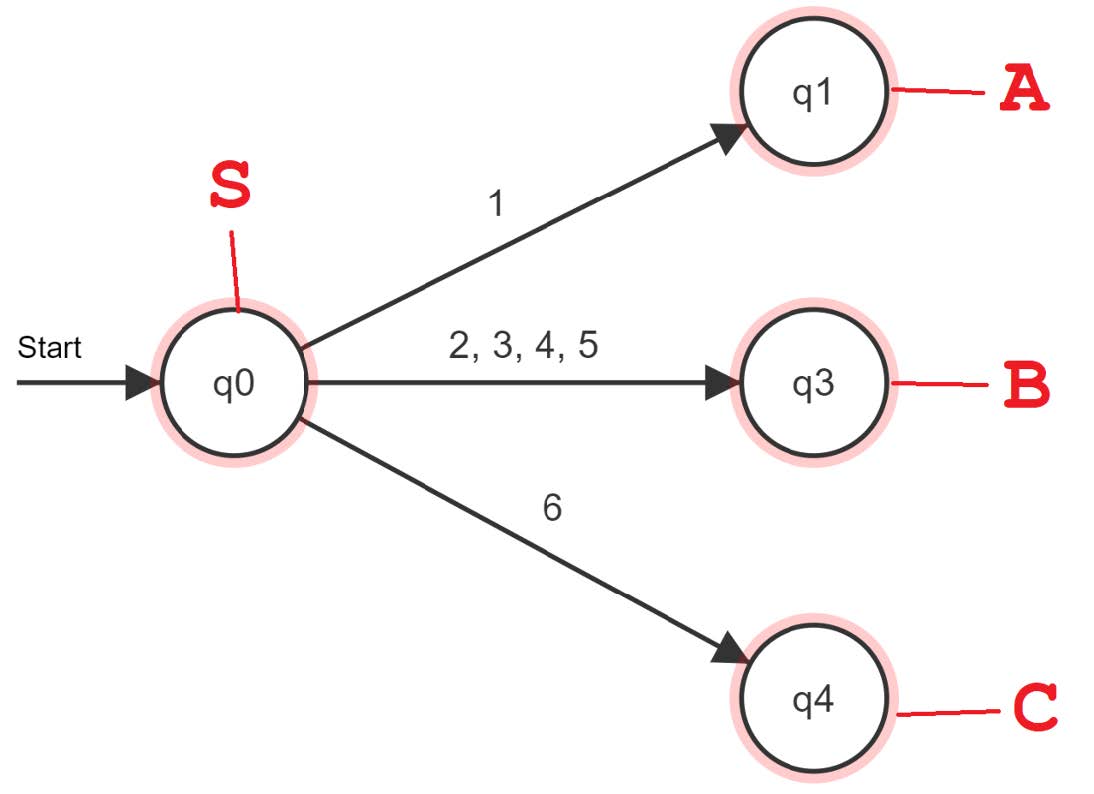
Da bereits einzelne Noten als fertige Terminale vom Startsymbol S aus eingesetzt werden können, müssen die Zustände q1, q2 und q3 auch Endzustände sein:
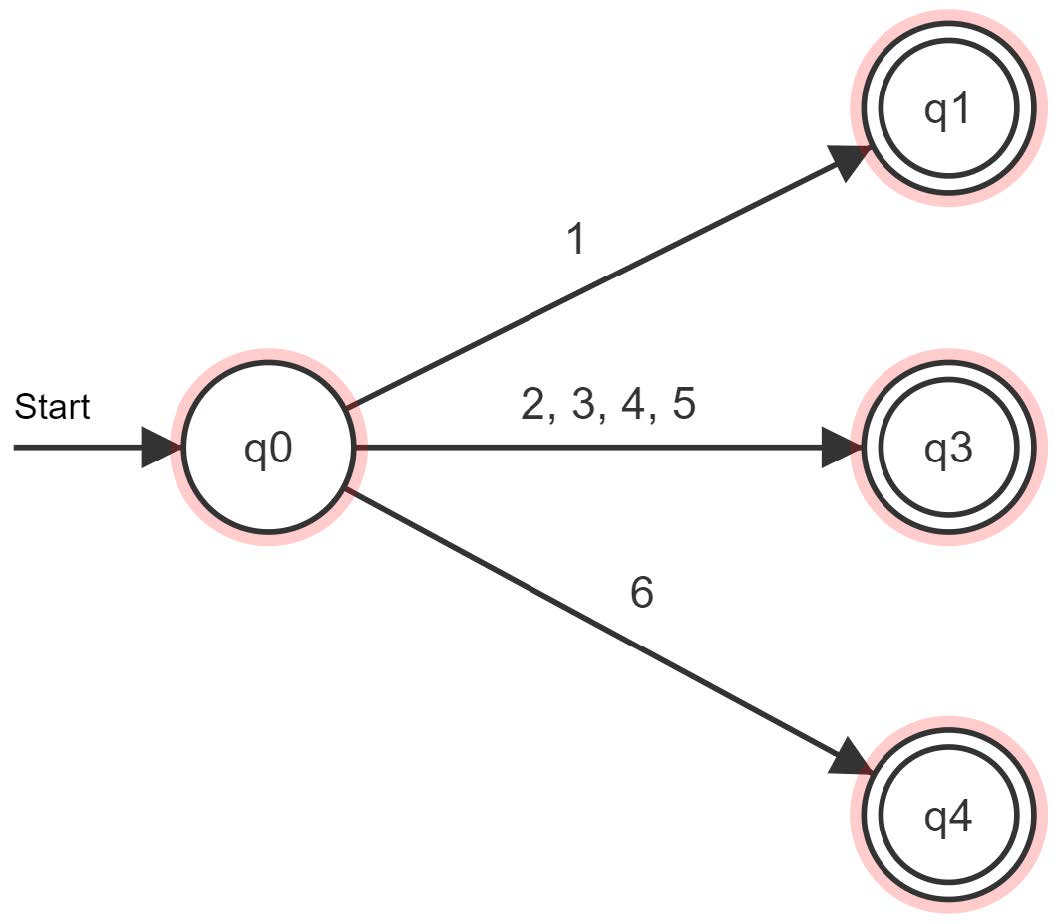
Jetzt geht es mit den Produktionsregeln A ➔ - , B ➔ +|- und C ➔ + weiter:
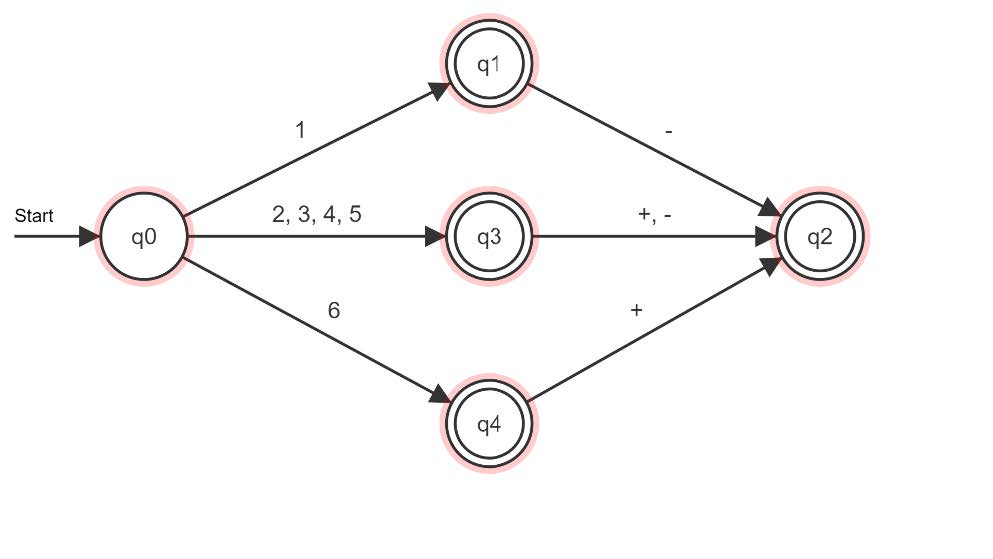
Und schon haben wir einen DEA entworfen, der ein Akzeptor für unsere reguläre Grammatik ist. Hieran kann man erkennen, dass es zu jedem Zustandsübergang beim DEA ein Äquivalent in den Produktionsregeln der Grammatik gibt und jede Produktionsregel hat ein Äquivalent in Form eines Zustandsübergangs beim DEA. Allgemein ist es so, dass es zu jeder regulären Sprache einen DEA gibt, der genau diese Sprache akzeptiert und auf der anderen Seite gibt es zu jedem DEA eine reguläre Sprache, deren Grammatik die von diesem DEA akzeptierte Sprache bildet. Somit kann man, wenn fraglich ist, ob eine Grammatik regulär ist, versuchen einen DEA zu entwerfen, der die Sprache der Grammatik akzeptiert.
Es gelten somit folgende Aussagen:
Eine Sprache ist genau dann regulär, wenn es eine reguläre Grammatik gibt, die diese Sprache
erzeugt.
Äquivalent hierzu ist:
Eine Sprache ist genau dann regulär, wenn es einen DEA gibt, der Akzeptor dieser Sprache ist.
- Entwickeln Sie einen DEA in Form eines Zustandsgraphens für das Uhrzeit-Beispiel.
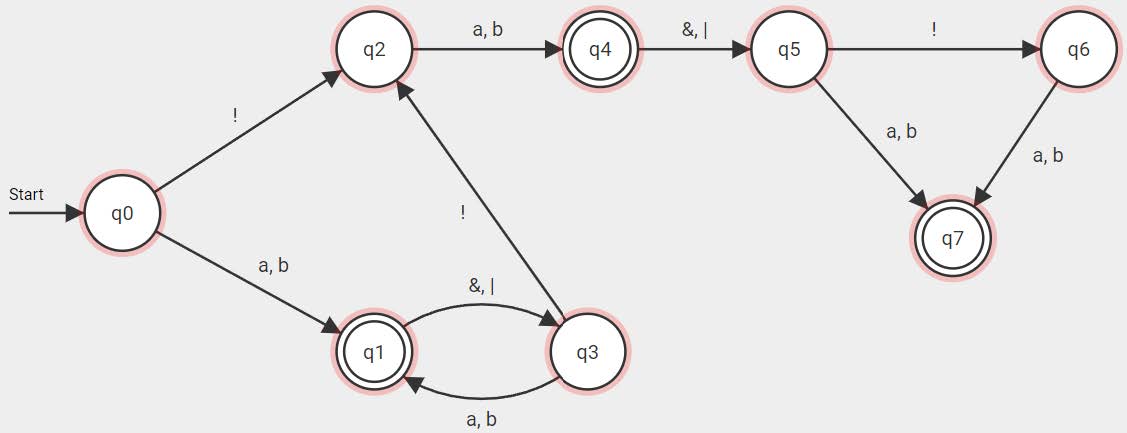
- Gegeben sei folgender Automat zum Erkennen boolescher Ausdrücke mit dem Eingabealphabet {a, b, &, |, !}.
- Beschreiben Sie, welche Sprache der DEA akzeptiert.
- Setzen Sie den Automaten in eine reguläre Grammatik um. (Alle nicht eingezeichneten Zustandsübergangen führen in einen Fehlerzustand.)
Setzen Sie sich zunächst inhaltlich mit dem Thema auseinander, indem Sie auf jeden Fall Aufgabe 1a und 2 machen (30Min).